Calculus III Summary
This page contains a list of tables that summarize the relationships between various ideas in multi-variable calculus (Calculus III). This is information is by no means complete. (I cannot emphasize this enough.) Examples of what’s not in the summary:
- Derivative rules of dot and cross products
- Cylinders and quadrics (Section 10.6) — table on page 557.
- Total differentials and all its uses
- linear approximation
- chain rule
- computing partial derivatives of one in terms of another (various variations on this problem)
- Critical points, minimization/maximization
- More…
Dot and Cross Products
| Dot | Cross | |
|---|---|---|
| Result | scalar-valued | vector-valued |
| Trig | {$\aa\dot\bb=|\aa|\;|\bb|\;\cos(\theta)$} {$\displaystyle \Rightarrow \cos(\theta)=\frac{\aa\dot\bb}{|\aa|\;|\bb|}$} | {$|\aa\cross\bb|=|\aa|\;|\bb|\;\sin(\theta)$} {$\displaystyle\Rightarrow \sin(\theta)=\frac{|\aa\cross\bb|}{|\aa|\;|\bb|}$} |
| Meaning | projection | (oriented) area of parallelogram |
| Application | {$W\text{ork} = \FF\dot\DD$} | {$\tau\text{orque}=\rr\cross\FF$} |
| Properties | {$\aa\dot\bb = \bb\dot\aa$} | {$\aa\cross\bb = -\bb\cross\aa$} In general, {$\aa\cross(\bb\cross\cc) \ne (\aa\cross\bb)\cross\cc$} |
| Orientation | {$\aa\dot\bb = 0 \quad \Rightarrow \quad \aa\perp\bb$} | {$\aa\cross\bb = \mathbf{0} \quad \Rightarrow \quad \aa\parallel\bb$} |
| Objects | Plane: {$\nn\dot(\rr-\rr_0)=\mathbf{0}$} | Line: {$\vv\cross(\rr-\rr_0)=0$} |
| Combinations | Volume of parallelepiped: {$\aa\dot(\bb\cross\cc) = (\aa\cross\bb)\dot\cc$} | |
| {$(\aa\dot\bb)^2 + |\aa\cross\bb|^2 = |\aa|^2|\bb|^2 \qquad$} (follows from {$\cos^2\theta + \sin^2\theta = 1$}) | ||
| {$\aa\cross(\bb\cross\cc) = (\aa\dot\cc)\bb - (\aa\dot\bb)\cc$} | ||
Compound operators and distances
| arbitrary {$\bb$} | unit {$\hb =\frac{\bb}{|\bb|}$} | 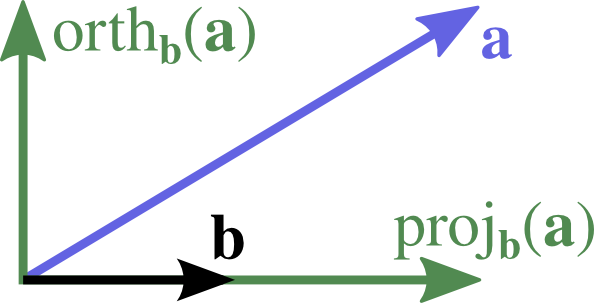 |
|
|---|---|---|---|
| {$\comp_\bb(\aa)$} | {$\displaystyle \frac{\aa\cdot\bb}{|\bb|}$} | {$\aa\cdot\hb$} | |
| {$\proj_\bb(\aa)$} | {$\displaystyle \big(\comp_\bb(\aa)\big) \frac{\bb}{|\bb|} = \frac{\aa\cdot\bb}{\bb\cdot\bb}\bb$} | {$(\aa\cdot\hb)\hb$} | |
| {$\orth_\bb(\aa)$} | {$\aa - \proj_\bb(\aa)$} | {$\aa - \proj_\hb(\aa)$} |
You only need to remember the third column! The second one follows using the transformation {$\hb=\frac{\bb}{|\bb|}$}.
| Distance between a point {$\pp$} and … | ||
|---|---|---|
| a point {$\qq$} | {$|\pp-\qq| = \sqrt{(\pp-\qq)\cdot(\pp-\qq)}$} | |
| a line through {$\qq$} in direction {$\vv$} | {$|\orth_\vv(\pp-\qq)|$} | |
| a plane through {$\qq$} with normal {$\nn$} | {$|\proj_\nn(\pp-\qq)| = |\comp_\nn(\pp-\qq)|$} | |
| an implicit surface {$g(x,y,z)=k$} | minimize {$|\pp-\vvec{x,y,z}|^2$} subject to constraint {$g(x,y,z)=k$} | |
Note that this table refers to points using their position vectors in order to use the vector operators.
Coordinate systems
| Cartesian | Cylindrical | Spherical | |
|---|---|---|---|
| Conversion | {$x = x$} {$y = y$} {$z = z$} | {$x = r\cos(\theta)$} {$y = r\sin(\theta)$} {$z = z$} | {$x = \rho\cos(\theta)\sin(\phi)$} {$y = \rho\sin(\theta)\sin(\phi)$} {$z = \rho\cos(\phi)$} |
| Ranges | {$x \in (-\infty, \infty)$} {$y \in (-\infty, \infty)$} {$z \in (-\infty, \infty)$} | {$r \in [0, \infty)$} {$\theta \in [0, 2\pi)$} {$z \in (-\infty, \infty)$} | {$\rho \in [0, \infty)$} {$\theta \in [0, 2\pi)$} {$\phi \in [0, \pi]$} |
| {$dV$} | {$dx\;dy\;dz$} | {$r\;dr\;d\theta\;dz$} | {$\rho^2\sin(\phi)\;d\rho\;d\theta\;d\phi$} |
Differentials/Integrals
| Area | {$dA = dx\;dy = r\;dr\;d\theta$} | {$\int_D dA = A(D) =$} area |
|---|---|---|
| Volume | {$dV = dx\;dy\;dz = r\;dr\;d\theta\;dz = \rho^2\sin\phi\;d\rho\;d\phi\;d\theta$} | {$\int_E dV = V(E) =$} volume |
| Line | {$d\rr = \rr'(t)dt = \TT ds$} {$ds = |\rr'(t)|dt = \TT \cdot d\rr$} | {$\int_a^b d\rr = \rr(b)-\rr(a) =$} displacement {$\int_a^b ds = $} arc length |
| Surface | {$d\SS = \rr_u\times\rr_v dA = \nn dS$} {$dS = |\rr_u\times\rr_v| dA = \nn \cdot d\SS$} | {$\int_S dS = A(S) =$} surface area |
Curves and Surfaces
| Representation | Tangent | Normal | Length/Area | |
|---|---|---|---|---|
| Parametric curve | {$\rr(t)$} | {$\rr'(t)$} {$\TT(t)=\frac{\rr'(t)}{|\rr'(t)|}$} | (2D) rotate tangent (3D) {$\NN(t)=\frac{\TT'(t)}{|\TT'(t)|}$} | {$\int_C ds = \int_C |\rr'(t)|\;dt$} |
| Parametric surface | {$\rr(u,v)$} | {$\rr_u$}, {$\rr_v$} | {$\displaystyle \nn = \frac{\rr_u\cross\rr_v}{|\rr_u\cross\rr_v|}$} | {$\int_S dS = \iint_D |\rr_u\cross\rr_v|\;dA$} |
| Level curves | {$f(x,y)=c$} | {$\left<dx,dy\right>$} or {$\left<1,\frac{dy}{dx}\right>$} or {$\left<\frac{dx}{dy},1\right>$} (slope = {$\frac{dy}{dx}$}) | {$\grad f$} | |
| Level surface | {$f(x,y,z)=c$} | If, implicitly, {$z=g(x,y)$}, then the tangents are {$\left<1,0,g_x\right>, \left<0,1,g_y\right>$}, where {$(g_x,g_y)=-\left(\frac{f_x}{f_z}, \frac{f_y}{f_z}\right)$}. | {$\grad f$} |
Generalizations of the Fundamental Theorem
To see the vector-inspired analogy, you should treat {$\grad$} as {$\left<\pdiff{}{x}, \pdiff{}{y}, \pdiff{}{z}\right>$}.
| Differential Geometry notation → |
{$\omega$} is a 0-form, 1-form, 2-form, or 3-form | {$d$} = exterior derivative on {$k$}-forms (manifests itself as {$\tgrad$}, {$\tcurl$}, and {$\tdiv$} on scalar-, vector-, and bivector-valued functions) | {$d\;d\omega = 0$} | ||
|---|---|---|---|---|---|
| signed value |
{$1$} | scalar | {$f$} | ||
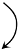 {$\grad$} {$\grad$} |
|||||
| oriented length |
{$\vv\;\;1 = \vv$} | vector | {$\tgrad f = \grad f$} | {$\curl \grad f = \mathbf{0}$} | |
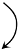 {$\curl$} {$\curl$} |
|||||
| oriented area |
{$\uu\cross\vv$} | bivector (vector-valued) | {$\tcurl \FF = \curl \FF$} | {$\div \curl \FF = 0$} | |
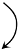 {$\div$} {$\div$} |
|||||
| signed volume | {$\ww\dot(\uu\cross\vv)$} | trivector (scalar-valued) | {$\tdiv \GG = \div \GG$} | ||
| Differential Geometry notation → |
Generalized Stokes' Theorem | {$\int_{\Omega} d\omega = \oint_{\partial\Omega} \omega$} |
|---|---|---|
| {$\grad$} | Fundamental Theorem of Calculus ({$f$} univariate) |
{$\int_{[a,b]} df = \int_a^b f'(x)dx = f(b) - f(a)$} |
| Fundamental Theorem of Line Integrals ({$f$} multivariate) |
{$\int_{C} (\grad f) \dot d\rr = f(\rr(b)) - f(\rr(a))$} | |
| {$\curl$} | Green's Theorem (2D) | {$\iint_{D} \left(\pdiff{Q}{x} - \pdiff{P}{y}\right) dA = \int_{\partial D} P\;dx + Q\;dy$} {$\iint_{D} (\curl \FF) \dot \mathbf{k} \;dA = \oint_{\partial D} \FF \dot d\rr = \oint_{\partial D} \FF \dot \TT ds$} |
| Stokes' Theorem (3D) | {$\iint_{S} (\curl \FF) \dot d\SS = \oint_{\partial S} \FF \dot d\rr = \oint_{\partial S} \FF \dot \TT ds$} | |
| {$\div$} | Green's Theorem variant (2D) | {$\iint_{D} \div \FF\;dA = \oint_{\partial D} \FF \dot \NN\;ds$} |
| Divergence Theorem (3D) | {$\iiint_{E} \div \FF\;dV = \iint_{\partial E} \FF \dot d\SS = \iint_{\partial E} \FF \dot \nn dS$} |
For each of {$\tgrad$}, {$\tcurl$}, and {$\tdiv$} above, the first fundamental theorem is a specialization of the second one that appears in the table cell below it.