Calculus III Summary
This page contains a list of tables that summarize the relationships between various ideas in Calculus III. This is information is by no means complete. (I cannot emphasize this enough.) Examples of what’s not in the summary:
- Derivative rules of dot and cross products
- Cylinders and quadrics (Section 10.6) — table on page 557.
- Total differentials and all its uses
- linear approximation
- chain rule
- computing partial derivatives of one in terms of another (various variations on this problem)
- Critical points, minimization/maximization
- More…
Dot and Cross Products
| Dot | Cross | |
|---|---|---|
| Result | scalar-valued | vector-valued |
| Trig | {$\aa\dot\bb=|\aa|\;|\bb|\;\cos(\theta)$} {$\displaystyle \Rightarrow \cos(\theta)=\frac{\aa\dot\bb}{|\aa|\;|\bb|}$} | {$|\aa\cross\bb|=|\aa|\;|\bb|\;\sin(\theta)$} {$\displaystyle\Rightarrow \sin(\theta)=\frac{|\aa\cross\bb|}{|\aa|\;|\bb|}$} |
| Meaning | projection | (oriented) area of parallelogram |
| Application | {$W\text{ork} = \FF\dot\DD$} | {$\tau\text{orque}=\rr\cross\FF$} |
| Properties | {$\aa\dot\bb = \bb\dot\aa$} | {$\aa\cross\bb = -\bb\cross\aa$} In general, {$\aa\cross(\bb\cross\cc) \ne (\aa\cross\bb)\cross\cc$} |
| Orientation | {$\aa\dot\bb = 0 \quad \Rightarrow \quad \aa\perp\bb$} | {$\aa\cross\bb = \mathbf{0} \quad \Rightarrow \quad \aa\parallel\bb$} |
| Objects | Plane: {$\nn\dot(\rr-\rr_0)=\mathbf{0}$} | Line: {$\vv\cross(\rr-\rr_0)=0$} |
| Combinations | Volume of parallelepiped: {$\aa\dot(\bb\cross\cc) = (\aa\cross\bb)\dot\cc$} | |
| {$(\aa\dot\bb)^2 + |\aa\cross\bb|^2 = |\aa|^2|\bb|^2 \qquad$} (follows from {$\cos^2\theta + \sin^2\theta = 1$}) | ||
| {$\aa\cross(\bb\cross\cc) = (\aa\dot\cc)\bb - (\aa\dot\bb)\cc$} | ||
Compound operators and distances
| arbitrary {$\bb$} | unit {$\hb =\frac{\bb}{|\bb|}$} | 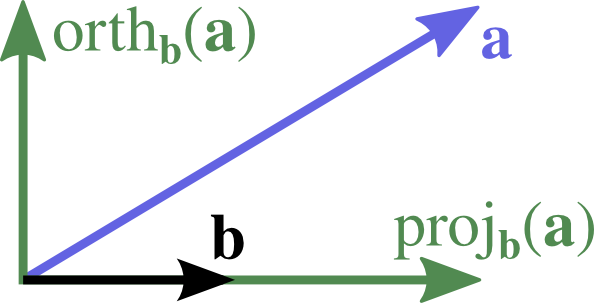 |
|
|---|---|---|---|
| {$\comp_\bb(\aa)$} | {$\displaystyle \frac{\aa\cdot\bb}{|\bb|}$} | {$\aa\cdot\hb$} | |
| {$\proj_\bb(\aa)$} | {$\displaystyle \big(\comp_\bb(\aa)\big) \frac{\bb}{|\bb|} = \frac{\aa\cdot\bb}{\bb\cdot\bb}\bb$} | {$(\aa\cdot\hb)\hb$} | |
| {$\orth_\bb(\aa)$} | {$\aa - \proj_\bb(\aa)$} | {$\aa - \proj_\hb(\aa)$} |
You only need to remember the third column! The second one follows using the transformation {$\hb=\frac{\bb}{|\bb|}$}.
| Distance between a point {$\pp$} and … | ||
|---|---|---|
| a point {$\qq$} | {$|\pp-\qq| = \sqrt{(\pp-\qq)\cdot(\pp-\qq)}$} | |
| a line through {$\qq$} in direction {$\vv$} | {$|\orth_\vv(\pp-\qq)|$} | |
| a plane through {$\qq$} with normal {$\nn$} | {$|\proj_\nn(\pp-\qq)| = |\comp_\nn(\pp-\qq)|$} | |
| an implicit surface {$g(x,y,z)=k$} | minimize {$|\pp-\vvec{x,y,z}|^2$} subject to constraint {$g(x,y,z)=k$} | |
Note that this table refers to points using their position vectors in order to use the vector operators.
Coordinate systems
| Cartesian | Cylindrical | Spherical | |
|---|---|---|---|
| Conversion | {$x = x$} {$y = y$} {$z = z$} | {$x = r\cos(\theta)$} {$y = r\sin(\theta)$} {$z = z$} | {$x = \rho\cos(\theta)\sin(\phi)$} {$y = \rho\sin(\theta)\sin(\phi)$} {$z = \rho\cos(\phi)$} |
| Ranges | {$x \in (-\infty, \infty)$} {$y \in (-\infty, \infty)$} {$z \in (-\infty, \infty)$} | {$r \in [0, \infty)$} {$\theta \in [0, 2\pi)$} {$z \in (-\infty, \infty)$} | {$\rho \in [0, \infty)$} {$\theta \in [0, 2\pi)$} {$\phi \in [0, \pi]$} |
| {$dV$} | {$dx\;dy\;dz$} | {$r\;dr\;d\theta\;dz$} | {$\rho^2\sin(\phi)\;d\rho\;d\theta\;d\phi$} |
Differentials/Integrals
| Area | {$dA = dx\;dy = r\;dr\;d\theta$} | {$\int_D dA = A(D) =$} area |
|---|---|---|
| Volume | {$dV = dx\;dy\;dz = r\;dr\;d\theta\;dz = \rho^2\sin\phi\;d\rho\;d\phi\;d\theta$} | {$\int_E dV = V(E) =$} volume |
| Line | {$d\rr = \rr'(t)dt = \TT ds$} {$ds = |\rr'(t)|dt = \TT \cdot d\rr$} | {$\int_a^b d\rr = \rr(b)-\rr(a) =$} displacement {$\int_a^b ds = $} arc length |
| Surface | {$d\SS = \rr_u\times\rr_v dA = \nn dS$} {$dS = |\rr_u\times\rr_v| dA = \nn \cdot d\SS$} | {$\int_S dS = A(S) =$} surface area |
Curves and Surfaces
| Representation | Tangent | Normal | Length/Area | |
|---|---|---|---|---|
| Parametric curve | {$\rr(t)$} | {$\rr'(t)$} {$\TT(t)=\frac{\rr'(t)}{|\rr'(t)|}$} | (2D) rotate tangent (3D) {$\NN(t)=\frac{\TT'(t)}{|\TT'(t)|}$} | {$\int_C ds = \int_C |\rr'(t)|\;dt$} |
| Parametric surface | {$\rr(u,v)$} | {$\rr_u$}, {$\rr_v$} | {$\displaystyle \nn = \frac{\rr_u\cross\rr_v}{|\rr_u\cross\rr_v|}$} | {$\int_S dS = \iint_D |\rr_u\cross\rr_v|\;dA$} |
| Level curves | {$f(x,y)=c$} | {$\left<dx,dy\right>$} or {$\left<1,\frac{dy}{dx}\right>$} or {$\left<\frac{dx}{dy},1\right>$} (slope = {$\frac{dy}{dx}$}) | {$\grad f$} | |
| Level surface | {$f(x,y,z)=c$} | If, implicitly, {$z=g(x,y)$}, then the tangents are {$\left<1,0,g_x\right>, \left<0,1,g_y\right>$}, where {$(g_x,g_y)=-\left(\frac{f_x}{f_z}, \frac{f_y}{f_z}\right)$}. | {$\grad f$} |
Generalizations of the Fundamental Theorem
To see the vector-inspired analogy, you should treat {$\grad$} as {$\left<\pdiff{}{x}, \pdiff{}{y}, \pdiff{}{z}\right>$}.
| Differential Geometry notation → |
{$\omega$} is a 0-form, 1-form, 2-form, or 3-form | {$d$} = exterior derivative on {$k$}-forms (manifests itself as {$\tgrad$}, {$\tcurl$}, and {$\tdiv$} on scalar-, vector-, and bivector-valued functions) | {$d\;d\omega = 0$} | ||
|---|---|---|---|---|---|
| signed value |
{$1$} | scalar | {$f$} | ||
 {$\grad$} {$\grad$} |
|||||
| oriented length |
{$\vv\;\;1 = \vv$} | vector | {$\tgrad f = \grad f$} | {$\curl \grad f = \mathbf{0}$} | |
 {$\curl$} {$\curl$} |
|||||
| oriented area |
{$\uu\cross\vv$} | bivector (vector-valued) | {$\tcurl \FF = \curl \FF$} | {$\div \curl \FF = 0$} | |
 {$\div$} {$\div$} |
|||||
| signed volume | {$\ww\dot(\uu\cross\vv)$} | trivector (scalar-valued) | {$\tdiv \GG = \div \GG$} | ||
| Differential Geometry notation → |
Generalized Stokes' Theorem | {$\int_{\Omega} d\omega = \oint_{\partial\Omega} \omega$} |
|---|---|---|
| {$\grad$} | Fundamental Theorem of Calculus ({$f$} univariate) |
{$\int_{[a,b]} df = \int_a^b f'(x)dx = f(b) - f(a)$} |
| Fundamental Theorem of Line Integrals ({$f$} multivariate) |
{$\int_{C} (\grad f) \dot d\rr = f(\rr(b)) - f(\rr(a))$} | |
| {$\curl$} | Green's Theorem (2D) | {$\iint_{D} \left(\pdiff{Q}{x} - \pdiff{P}{y}\right) dA = \int_{\partial D} P\;dx + Q\;dy$} {$\iint_{D} (\curl \FF) \dot \mathbf{k} \;dA = \oint_{\partial D} \FF \dot d\rr = \oint_{\partial D} \FF \dot \TT ds$} |
| Stokes' Theorem (3D) | {$\iint_{S} (\curl \FF) \dot d\SS = \oint_{\partial S} \FF \dot d\rr = \oint_{\partial S} \FF \dot \TT ds$} | |
| {$\div$} | Green's Theorem variant (2D) | {$\iint_{D} \div \FF\;dA = \oint_{\partial D} \FF \dot \NN\;ds$} |
| Divergence Theorem (3D) | {$\iiint_{E} \div \FF\;dV = \iint_{\partial E} \FF \dot d\SS = \iint_{\partial E} \FF \dot \nn dS$} |
For each of {$\tgrad$}, {$\tcurl$}, and {$\tdiv$} above, the first fundamental theorem is a specialization of the second one that appears in the table cell below it.